Vorið 1904 gekk hinn snjalli franski stærðfræðingur Henri Poincaré um og gruflaði í vandamáli sem hann fann enga lausn á. Það fólst í að lýsa eiginleikum rúmfræðilegra forma í æðri víddum. Poincaré hafði hugmynd um hvernig formin myndu verða en gat ekki sannað það.
Þess vegna setti hann fram svonefnda tilgátu Poincarés, sem hefur síðan orðið ein helsta gáta stærðfræðinnar.
Ótal stærðfræðingar hafa brotið heilann – og þolinmæði fjölskyldunnar – í leitinni að svarinu við þessari frægu tilgátu. Reyndar er talað um heilkennið Poincaritis meðal fagmanna, sem ástand þeirra er ekki geta slitið sig frá vandamálinu.
Nú bendir margt til að leitinni sé loks lokið. Árið 2002 kom rússnenski stærðfræðingurinn Grigori Perelman með lausn á vandamálinu. Hann setti lausnina ekki fram í grein í vísindatímariti, sem annars er vaninn, heldur lagði fram þrjár greinagerðir út á Netið.
Perelman fylgdi þessu eftir með fyrirlestrarferð í Bandaríkjunum, en síðan hefur harla lítið heyrst frá honum. Á meðan hafa bestu stærðfræðingar heims grannskoðað flókna sönnunarfærslu Perelmans og nú þegar hafa komið fram meira en eittþúsund síður þéttritaðar umsögnum og útreikningum.
Og niðurstaðan er að svar Rússans er í raun gott og gilt.
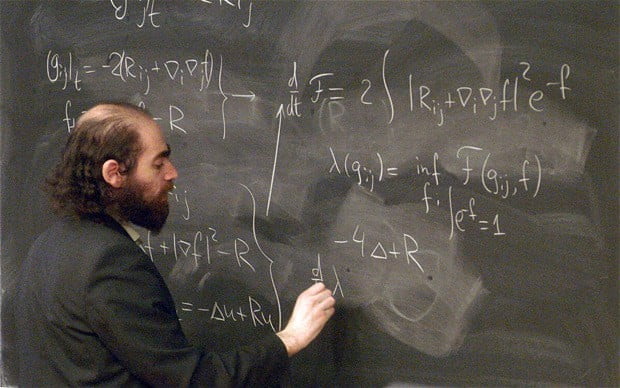
Með framtaki sínu getur Perelmann gert tilkall til verðlauna sem nema einni milljón dölum. Bandaríska stofnunin Clay Mathematics Institute hefur heitið slíkum verðlaunum fyrir hverja lausn á sjö sígildum gátu stærðfræðinnar.
Perelman hefur bara engan áhuga. Áður hefur hann afþakað Fields – verðlaunin sem innan stærðfræðinnar jafngilda Nóbelsverðlaununum. Óvíst er hvaða ástæður liggja að baki ákvörðun Perelmanns en mögulega tengist það óánægju hans með þau siðferðisviðmið er ríkja í heimi stærðfræðinnar.
Snillingur hafnar metorði
Annars á hann sannarlega allan heiður skilinn. Aðeins sextán ára gamall vann Perelman til gullverðlauna í ólympísku stærðfræðikeppninni og náði þar hámarksárangri. Síðan hefur hann átt frábæran starfsferil, sem endaði með lausn hans á tilgátu Poincarés eftir sjö ára þrotlaust starf.
En eftir þessa frábæru framistöðu hefur Grigori Perelmann dregið sig úr sviðsljósinu. Sagt er að hann noti tíma sinn nú í gönguferðir í nágrenni St. Pétursborgar, þar sem hann býr í lítilli íbúð með móður sinni.
Hann er lítið gefinn fyrir að koma fram opinberlega og hefur sagt: „Ég tel ekki að nokkuð af því sem ég segi sé áhugavert fyrir opinbera aðila.“ Hafi Rússinn í raun og veru ákveðið að leggja stærðfræðina á hilluna hafa vísindin glatað einum snjallasta manni sínum. Þó er einnig mögulegt að hann hafi einangrað sig til að kljást við enn eina stærðfræðiþrautina.
Þrátt fyrir að Perelman sé úr myndinni verður tilgáta Poincarés nú að teljast leyst. Eftir standa aðrar sex gátur, sumar þeirra meira en 100 ára gamlar.
Allar eiga þær sameiginlegt að vera harla snúnar. Það eitt að skilja spurningarnar getur reynst erfitt fyrir leika, og jafnvel lærðustu stærðfræðingar eiga erfitt með að finna svörin. Sumar gáturnar eru ansi ergilegar.
Sönnunin getur virst innan seilingar, en er það ekki. Sem dæmi varðar Rieman – tilgátan dreifingu prímtalna (tölur sem einungis er hægt að deila í með einum og þeim sjálfum, sem dæmi 5 og 7).
Tilgátan hefur verið sannreynd fyrir fyrsta einn og hálfan milljarð lausna í tiltekinni jöfnu með góðum árangri. En það er erfðiðara að sanna að þetta gildi um allar prímtölur og sönnun er nauðsynleg, því stærðfræðin hefur að geyma fjölmörg dæmi um mynstur sem virðast vera regluleg en síðan koma skyndilega fram frávik.

Evklíð ruddi brautina
Sannanir hafa alltaf gengt mikilvægu hlutverki í stærðfræðinni, því þær geta skorið úr um ýmis ágreiningsefni. Þær eiga sér merka sögu. Grikkir fornaldar voru hinir fyrstu til að gera sér grein fyrir mikilvægi þeirra.
Þrátt fyrir að fræði þeirra hafi ekki öll staðist tímanns tönn, gegnir öðru máli um uppgötvanir innan stærðfræðinnar.

Gott dæmi er ein frægasta sönnun Evklíðs sem varðar prímtölur. Fyrir meira en 2300 árum sannaði Evklíð að til er óendanlegur fjöldi prímtalna.
Sönnunin er fallega einföld: ef maður ímyndar sér að einhver segist búa yfir lista með öllum prímtölum, getur maður ætíð sannað að það skorti eina. Maður tekur nefnilega allar prímtölur listans, margfaldar þær saman og bætir 1 við.
Niðurstöðuna er ekki hægt að deila í með nokkurri tölu úr listanum því það verður ævinlega 1 í afgang. Þetta þýðir að hin nýja tala hlýtur að vera prímtala.
Niðurstaðan er því að einu má gilda hversu margar prímtölur finnast, þær hljóta alltaf að vera fleiri og því hlýtur fjöldi þeirra að vera óendanlegur.
Sönnun Evklíðs er algerlega pottþétt og það þarf ekkert nema heilbrigða skynsemi til að skilja hana. Sú er sjaldnast raunin með stærðfræði nútímans.
Jafnvel eftir þriggja ára vinnu geta sumir af fremstu stærðfræðingum heims ekki kveðið úr um með fullri vissu hvort sönnun Perelmans sé rétt og þetta er hreint ekki óvanalegt.
Stærðfræði er orðin svo flókin nú á dögum að það ríkir oft óvissa um sannanir. Árið 1982 varð opinberuð sönnun um að unnt sé að gera kerfi til greininga á svonefndum endanlegum einföldum grúpum, eins konar lotukerfi fyrir stærðfræðilegar samhverfur. Sönnuninni fylgdi meira en 10 þúsund síður. Undir lok síðustu aldar kom í ljós að hún var ekki tæmandi. Hún var síðan betrumbætt árið 2004 og viðbæturnar einar voru tólf hundruð blaðsíður.
Í ljósi þess er engin trygging fyrir því að allar þær gátur sem Clay Mathematics Institute veitir verðlaunum fyrir verði nokkru sinni leystar – eða að þær séu leysanlegar.
Áður en Perelmann lagði fram greinagerðir sínar ríkti einnig vafi á hvort hægt væri að sanna tilgátu Poincarés. Bruce Kleine við Yale University sem hefur eytt þremur árum í að kanna lausnina, sagði: „Það gæti gerst innan 100 ára – eða aldrei.“
En svo virðist sem Grigory Perelmann hafi tekist þetta. Og fordæmi hans veitir öðrum stærðfræðingum haldbetri vonir um að leysa megi fleiri gátur. En þrátt fyrir að Perelmann hafi komið með mótefni gegn poincaritis – heilkenninu, er ennþá fullt af vandamálasýklum stærðfræðinnar sem geta smitað mann.



