Þversagnir eru mótsagnakenndar staðhæfingar og að því er virðist rökræn hugsun sem leiðir til órökréttar eða tilgangslausra ályktana. Hér færðu skýringu á stærstu þversögnum vísinda síðustu 2500 ár.
RÖKFRÆÐI

Þversögn lygarans afhjúpar að staðhæfing getur verið að hluta til sönn og að hluta til ósönn. Þetta hefur skapað nýja tölvurökfræði sem fær m.a. ákvarðanir róbóta til að virðast mannlegri.
Lygar gera tölvur mennskari
Hugmynd: 400 f.Kr.
„Þessi setning er ósönn“ er ein útgáfa af svokallaðri þverstæðu lygarans þar sem staðhæfing myndar órjúfanlega keðju af rökfærslum sem ganga í hring. Því ef setningin er ósönn er hún jú sönn en ef hún er sönn er hún vitanlega ósönn.
Þverstæða þessi er kennd við forngrikkjann Eubulites sem kom fram með eftirfarandi spurningu: „Ef maður segist ljúga, er það sem hann segir satt eða ósatt?“ Slíkar mótsagnir má leiða út t.d. með: „Næsta setning er sönn. Fyrri setning er ósönn.“
Þverstæðan hefur leitt til þess að sumir rökfræðingar hafa lagt til hliðar hugmyndina um tvígildi eða að setningar séu ýmist sannar eða ósannar. Þess í stað má veita þeim öllum gildi milli tveggja andstæða. Setning getur t.d. verið að hluta til sönn eða hún getur verið að hluta til blanda af tveimur staðhæfingum. Þetta er t.d. þekkt í andlitskennslaburði.
Þekktasta rökfræði sem byggir ekki á tvígildi er svonefnd fuzzy-logic. Slík rökfræði nýtist í forritun á tauganeti og gervigreind því hún örvar ákvörðunarferla sem minna á innsæi manna.
RÖKFRÆÐI

Ómögulegi þríhyrningurinn er einungis mögulegur í raunveruleikanum þegar horft er á hann frá tilteknu sjónarhorni (innsett).
Ómögulegur þríhyrningur gabbar heilann
Hugmynd: 1934
„Ómögulegur í sínu hreinasta formi“ nefndi breski stærðfræðingurinn Roger Penrose fyrirbærið. Þessi ómögulegi þríhyrningur var í fyrsta sinn teiknaður af sænska listamanninum Oscar Reutersvärd árið 1934 og varð vinsæll í meðförum Penrose og hollenska listamannsins Escher. Fígúran er sjónhverfing sem líkist þrívíðum þríhyrningi þegar það er teiknað í tveimur víddum en getur ekki fyrirfundist í þremur víddum raunveruleikans.
Við fyrstu sýn virðist þríhyrningurinn skynsamlegur en það er ómögulegt að fylgja flötum hans alla leið með augunum; t.d. getur neðsti bjálkinn litið út fyrir að vera bæði fyrir framan og aftan efsta punkt þríhyrningsins.
Vitundarfræðingar hafa rannsakað getu heilans til þess að horfa á þennan ómögulega þríhyrning sem þrívíðan, jafnvel eftir að búið er að rjúfa sjónhverfinguna. Tilraunirnar styðja sálfræðilega kenningu um að hugræn geta mannsins skiptist í að hluta til sjálfstæðar einingar. Sjónræna einingin heldur þannig áfram að sjá þríhyrninginn sem fyrirbæri þrátt fyrir að vitundin hafi afhjúpað missýninguna.
EÐLISFRÆÐI
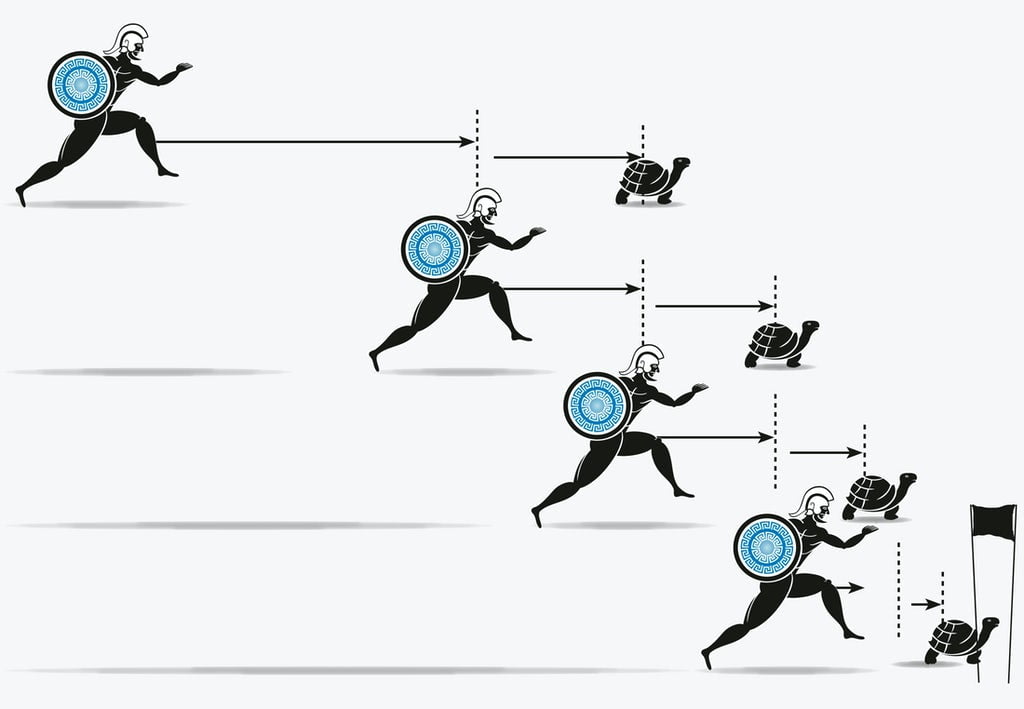
Akkilles gaf skjaldbökunni 100 metra forskot. Meðan hann hleypur þá 100 metra nær skjaldbakan 10 metra fram á við. Meðan hann hleypur þá 10 metra nær skjaldbakan 1 metra o.s.frv. Akkilles nær því aldrei skjaldbökunni.
Hlauparinn nær aldrei skjaldbökunni
Hugmynd: 400 f.Kr.
Goðsagnahetjan Akkilles fer í veðmál við skjaldböku. Akkilles er viss um sigur og veitir skjaldbökunni forskot sem nemur t.d. 100 metrum.
Meðan Akkilles hleypur þessa 100 metra hefur skjaldbakan náð að fara aðra 10 metra fram á við. Þegar Akkilles hleypur þá 10 metra nær skjaldbakan enn 1 metra. Þegar Akkilles hleypur þennan 1 metra nær skjaldbakan 10 cm lengra o.s.frv.
Afleiðingin af þessari hugarsmíð er að Akkilles nær aldrei skjaldbökunni, hann kemst bara nær og nær henni. Almenn skynsemi sannfærir okkur þó um að það sé eitthvað rangt við þetta reikningsdæmi og nútíma stærðfræði skýrir það.
Núna hafa stærðfræðingar leyst þverstæðuna með hugtakinu jaðargildi. Í heimi Zenons gat helmingurinn af leiðinni, mínus fjórðungur, mínus áttundapartur o.s.frv. aldrei orðið núll. En núna vitum við að 0,0…1 – þar sem punktarnir tákna óendanlegan fjölda núlla – er nákvæmlega sama og 0, því við náum aldrei til tölunnar 1.
EÐLISFRÆÐI

Alheimur er þegar óendanlegur en þenst engu að síður stöðugt út. Sumir óendanleikar eru þannig stærri en aðrir.
Óendanleiki finnst í mörgum stærðum
Hugmynd: 1873
Í hversdagslífinu er sagt að heildin sé ævinlega stærri en einstakir hlutar hennar en í stærðfræðinni er þessu öðruvísi farið. Þverstæðan kemur í ljós þegar litið er til talna.
Tölur sem má tákna með bilum á línu kallast rauntölur. Það eru allar tölur sem má skrifa með brotatölum, með allt að óendanlega mörgum tölum. 2 og 78,4297 og talan pí (3,14…) sem tjáir sambandið milli ummáls hrings og þvermáls eru allt rauntölur.
Stærðfræðilega má sanna að það eru óendanlega margar rauntölur á milli 0 og 1. þ.e.a.s. fleiri en hægt er að telja með náttúrulegum tölum – öllum jákvæðum heilum tölum eins og 1, 2, 27 og 1.158 – sem einnig í sjálfu sér mynda óendanlega runu. Óendanlegt magn af náttúrulegum tölum er hlutmengi í óendanlegu magni af rauntölum, m.ö.o. finnast margar gerðir af óendanleika og sumir óendanleikar eru stærri en aðrir.
Þetta sýndi þýski stærðfræðingurinn Georg Cantor með annarri hornalínuaðferð Cantors þegar hann lagði grunninn að nútíma mengjafræði upp úr 1880.
Bæði hlutmengi og heild eru óendanleg
Mengi náttúrulegra talna (1, 2, 3 o.s.frv.) er hlutmengi rauntalna (stóri hringurinn), en bæði mengin eru óendanleg. Svo það eru til nokkrar tegundir af óendanleika, og sumir óendanleikar eru meiri en aðrir.
Náttúrulegar tölur
Náttúrulegar tölur eru allar jákvæðar heiltölur – þær sem við notum dagsdaglega til að telja með. Mismunandi greinar stærðfræðinnar eru ekki á einu máli um hvort 0 teljist vera náttúruleg tala.
Heilar tölur
Heilar tölur eru allar þær tölur sem hægt er að skrifa án þess að nota brot eða aukastafi, þ.e.a.s. að heilu tölurnar innihalda einnig 0 og allar neikvæðar tölur.
Ræðar tölur
Ræðar tölur eru allar heilar tölur sem má skrifa sem brot og allar tölur sem má skrifa sem blöndu af heilum tölum og brotum.
Rauntölur
Rauntölur eru allar þær tölur sem má skrifa sem brotatölur með allt að óendanlega mörgum aukastöfum. Talan pí – 3,14159265… – er t.d. rauntala.
Bæði hlutmengi og heild eru óendanleg
Mengi náttúrulegra talna (1, 2, 3 o.s.frv.) er hlutmengi rauntalna (stóri hringurinn), en bæði mengin eru óendanleg. Svo það eru til nokkrar tegundir af óendanleika, og sumir óendanleikar eru meiri en aðrir.
Náttúrulegar tölur
Náttúrulegar tölur eru allar jákvæðar heiltölur – þær sem við notum dagsdaglega til að telja með. Mismunandi greinar stærðfræðinnar eru ekki á einu máli um hvort 0 teljist vera náttúruleg tala.
Heilar tölur
Heilar tölur eru allar þær tölur sem hægt er að skrifa án þess að nota brot eða aukastafi, þ.e.a.s. að heilu tölurnar innihalda einnig 0 og allar neikvæðar tölur.
Ræðar tölur
Ræðar tölur eru allar heilar tölur sem má skrifa sem brot og allar tölur sem má skrifa sem blöndu af heilum tölum og brotum.
Rauntölur
Rauntölur eru allar þær tölur sem má skrifa sem brotatölur með allt að óendanlega mörgum aukastöfum. Talan pí – 3,14159265… – er t.d. rauntala.
Skilningur Cantors á margs konar óendanleika byggir á starfi ítalska stærðfræðingsins og eðlisfræðingsins Galileo Galilei. Galilei sá að þrátt fyrir að magn ferningtalna, þ.e.a.s 1, 4, 9, 16 o.s.frv. er hlutmengi af þeim náttúrulegu tölum hljóta þessar tvær tölur að vera jafn stórar. Hverja einustu náttúrulegu tölu má nefnilega para við sína eigin ferningstölu, eða 1 með 1, 2 með 4, 3 með 9 o.s.frv.
Alheimur sýnir ennfremur að það má finna fleiri gerðir af óendanleika í raunheimi. Athuganir benda nefnilega greinilega til þess að hann er bæði óendanlegur og að þenjast stöðugt út.
EÐLISFRÆÐI

Skip hetjunnar Þeseusar var varðveitt og þvi viðhaldið í langan tíma. Að lokum var ekkert eftir af upprunalega skipinu.
Skip Þeseusar skiptist í tvö
Hugmynd: 500 f.Kr.
Í grískri goðafræði siglir þjóðhetjan Þeseus heim frá Krít í skipi sem síðan liggur í höfn Aþenu í margar aldir. Veður og vindar og tímans tönn vinna smám saman á skipinu þannig að á endanum er búið að skipta út hverjum einasta planka þar til ekkert er eftir af upprunalegu skipinu. En er það samt sem áður sama skipið eða er það nýtt skip? Og hvenær átti þá sú breyting sér stað?
Heraklítos, Platón og Plútark hafa allir spreytt sig á þessari frásögn. Enda virðist þarna vera grundvallarvandamál við skilgreiningu á hugtakinu samsemd yfir lengri tíma. Þverstæðan gegnir einnig hlutverki varðandi það hvaða augum við lítum manninn. Nánast engar frumur lifa frá fæðingu hans til dauða og hvað er það sem gerir okkur að sama einstaklingnum út allt lífið? Og hvað ef dag einn verður hægt að yfirfæra vitund okkar í tölvu?
Breski heimspekingurinn Thomas Hobbes flækti þversögnina enn frekar með sögu um sjómann sem safnar öllum plönkum sem skipt hafði verið út í skipi Þeseusar þar til hann getur endursmíðað það. Hvort þessara skipa er þá skip Þeseusar?
EÐLISFRÆÐI

Í myndinni „Aftur til framtíðar“ ferðast aðalpersónan aftur í tímann og tryggir þannig gæfulegri nútíð fyrir foreldra sína. Samkvæmt fræðimönnum mun sagan þó ævinlega þróast í átt að upprunalegu nútíðinni.
Orsakalykkja á ekkert upphaf
Hugmynd: 1781
Þinn eldri þú birtist skyndilega með teikningar að tímavél svo þú getur smíðað hana og síðar – þegar þú ert sjálfur orðinn þitt eldra ég – getur ferðast aftur til þíns yngra égs með sömu teikningar.
Sagan lýsir svokallaðri lokaðri orsakalykkju án upphafspunkts. Þverstæðan er eignuð Rudolf Erich Raspe, höfundi sagnanna um baróninn von Munchausen sem dró sjálfan sig upp á hárinu sem var þannig bæði orsök og verkun.
Orsakalykkjur eru vinsælar í kvikmyndum og bókum um tímaferðalög en eru jafnframt áhugavert rannsóknarsvið. Árið 2020 birtu vísindamenn við University of Queensland grein sem sýnir stærðfræðilega að raunveruleikinn muni leiðrétta sjálfan sig þannig að lykkjan leiði ekki til þverstæðu.
Fræðingarnir spá því að þrátt fyrir að upprunaleg orsök sé fjarlæg – t.d. fyrsti sjúklingurinn sem smitaðist með Covid-19 – munu síðari atvik leita í átt að raunverulegri nútíð. Þetta felur í sér að önnur manneskja verði þess í stað sú fyrsta til að smitast en að sagan muni síðan þróast til að verða líkari hinni upprunalegu.



